Spule und Transformator
Die Spule ist ein Bauteil, welches das Gegenstück zum Kondensator bildet. Während ein Kondensator Energie im elektrischen Feld speichert, so speichert eine Spule Energie im magnetischen Feld.
Funktionsweise
Fliesst ein elektrischer Strom entsteht ein Magnetfeld. Dieses Magnetfeld kann andere Leiter beeinflussen und in denen wiederum einen elektrischen Strom fliessen lassen. Durch die Aufwicklung des Leiters in der Luft oder ein geeignetes Objekt kann das Feld verstärkt werden. Des weiteren führt dies dazu, dass das Feld den eigenen Leiter beeinflusst.
Nach der Lenz'schen Regel wird durch eine Änderung des magnetischen Flusses durch eine Leiterschleife
eine Spannung induziert, so dass der dadurch fließende Strom ein Magnetfeld erzeugt,
welches der Änderung des magnetischen Flusses entgegenwirkt,
ggf. verbunden mit mechanischen Kraftwirkungen.
Einfach gesagt führt dies dazu, dass sich die Spule gegen Änderungen im Elektromagnetischen Feld zur wehr setzt.
Je schneller man versucht das Feld zu ändern desto grösser ist der Widerstand.
Strom in der Spule

Definition
Eine Spule hat eine Induktivität von 1 Henry, wenn bei gleichförmiger Stromänderung von 1 Ampere in 1 Sekunde eine Selbstinduktionsspannung von 1 Volt entsteht.
`1H=1(Vs)/A=1Ωs`
Induktivität
Die Fähigkeit Energie im magnetischen Feld zu speichern wird als Induktivität bezeichnet.
Induktivität trägt das Formelzeichen `L` (zu Ehren von Heinrich Friedrich Emil Lenz)
und die Einheit Henry `H`, benannt nach Joseph Henry welcher die elektromagnetische Selbstinduktion entdeckt hat.
Die Induktivität einer Spule ist von vier Faktoren abhängig
-
Permeabilitätszahl: Diese gibt an wie gut eine Spule geeignet ist für ein Magnetfeld.
Je höher, desto mehr Energie kann im Magnetfeld gespeichert werden.
Die Zahl fungiert als Multiplikator zur Magnetischen Fluxkonstante
(siehe Formelsammlung).
Formelzeichen: `mu_r`
Einheit: Dimensionslos -
Querschnittsfläche: Je grösser der Querschnitt der Spule, desto grösser die Induktivität.
Formelzeichen: A
Einheit: m2 -
Länge: Je kürzer die Spule, desto grösser die Induktivität.
Formelzeichen: `l`
Einheit: m -
Windungszahl: Je mehr Windungen, desto grösser die Induktivität
Formelzeichen: `N`
Einheit: Dimensionslos
Die Induktivität wird mittels folgender Formel berechnet:
`L=(mu_0*mu_r*A*N^2)/l`
Die Formel zeigt uns, dass die Induktivität grösser wird wenn die Windungszahl erhöht wird,
und/oder die Länge verkürzt wird.
Hinweis: Bei Spulen die um einen Ring gewickelt sind, gilt `l=pi*D` wobei "D" der mittlere Durchmesser ist.
Spule an Gleichstrom

Es spielt keine Rolle ob der Widerstand vor, oder nach der Spule in der Schaltung ist.
Eine Spule gilt als geladen nach `5*tau` Sekunden,
das magnetische Feld ist dann gesättigt.
Bei der Ladung folgt der Strom einer logarithmischen Kurve.
Zuerst ist der Strom sehr gross, nimmt aber mit der Zeit ab.
Die gemessene Spannung über der Spule folgt einer gespiegelten Kurve.
Die Berechnung der Spannung zu einem bestimmten Wert erfolgt mittels
`U_L=U*(1-e^(-t/tau))` wobei `U` die Endspannung ist, `e` die Eulersche Zahl (siehe Formelsammlung),
`t` die Zeit in Sekunden, und `tau` die Zeitkonstante.
Wird Spannung und Strom während dem Laden aufgezeichnet, so entstehen folgende Graphen:

Aus dieser Grafik ist ersichtlich, dass Spannung und Strom sich umgekehrt zueinander verhalten. Wird die maximale Spannung und der Maximale Strom auf einer Skala von 0%-100% gezeichnet, so ergibt die Summe zu einem Zeitpunkt jeweils 100%. Ist die Spule also 30% geladen, fliesst ein Ladestrom der 70% des Maximalstromes beträgt.
Prozentualwerte für Tau
| `tau` | Spannung | Strom |
|---|---|---|
| ≈0.7 | 50% | 50% |
| 1 | 36.8% | 63.2% |
| 2 | 13.5% | 86.5% |
| 3 | 5% | 95% |
| 4 | 1.8% | 98.2% |
| 5 | 0.7% | 99.3% |
Diese Tabelle und die Grafik oberhalb gelten für das Laden und Entladen beim Gleichstrom. Beim Laden sind die Zahlen und Grafik für Strom und Spannung exakt wie angegeben. Beim Entladen ist die Grafik für den Strom wie angegeben. Die Spannung ist umgekehrt da Spannung beim Entladen abgebaut und nicht aufgebaut wird. 63.2% bei 1 tau bedeutet hier, dass das Bauteil so viel Spannung bereits abgebaut hat.
Induzierte Spannung
Ist die Induktivität bekannt, kann berechnet werden wie viel Spannung induziert wird
wenn sich der Strom in einer bestimmten Zeit ändert.
Die Formel hierfür ist `U_0=-L*(DeltaI)/(Deltat)`
Wenn sich in einer Spule von 2 Henry also der Strom um 3A in 1.5 Sekunden ändert,
so ist die Induzierte Spannung 4 Volt.
Umstellungen
Induktivität ermitteln: `L=-U_0/((DeltaI)/(Deltat))`
Stromänderung ermitteln: `DeltaI=U_0/-L*Deltat`
Zeit ermitteln: `Deltat=(-L)/U_0*DeltaI`
Hinweis: Die Induktivität wird hier negativ angegeben da die induzierte Spannung entgegengesetzt fliesst.
Serielle und parallele Schaltungen
Serielle und parallele Schaltungen von Spulen werden exakt wie serielle und parallele Schaltungen von Widerständen gerechnet. Dies bedeutet, dass sich die Induktivitäten von Spulen in seriellen Schaltungen addieren. Bei parallelen Schaltungen kann eine von drei Formeln verwendet werden.
Einfache Formel
`L=L_1/n`
Diese Formel funktioniert wenn alle parallelen Spulen die exakt selbe Induktivität haben. In diesem Falle ist `L_1` die Induktivität einer der Spulen und `n` die Anzahl der Spulen.
Formel für zwei Spulen
`L=(L_1*L_2)/(L_1+L_2)`
Immer noch relativ einfach zu rechnen, funktioniert auch wenn die beiden Spulen verschiedene Induktivitäten haben, aber nur wenn es exakt zwei Spulen sind.
Universale Formel
`L=1/(1/L_1+1/L_2+...)`
Diese Formel funktioniert für eine beliebige Anzahl an Spulen mit beliebigen Induktivitäten.
Tip: `1/n` ist das Selbe wie `n^-1`. Die Formel oberhalb kann also umgeschrieben werden auf
`L=(L_1^-1+L_2^-1+...)^-1`. Diese Form ist ggf. einfacher in den Taschenrechner einzugeben.
Wechselspannung
Spulen im Gleichstromkreis erreichen ihren vollen Lade-, oder Entladezustand nach ca. 5 Tau. Im Wechselstromkreis ändert sich der Ladezustand einer Spule kontinuierlich. Da der Lade-, und Entladestrom einer Spule nicht immer gleich ist, sondern vom Ladezustand abhängig ist, fungiert dieser wie ein sich dynamisch verändernder Widerstand.
Zeichnet man Spannung und Strom im Wechselstromkreis über Zeit auf,
so entsteht der hier gezeigte Verlauf,
wobei blau die Spannung ist, und rot der Strom.
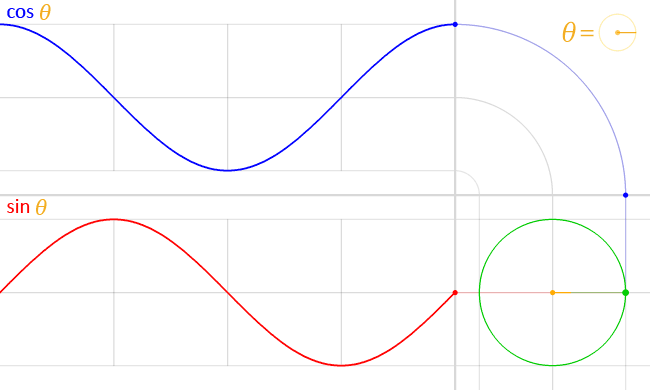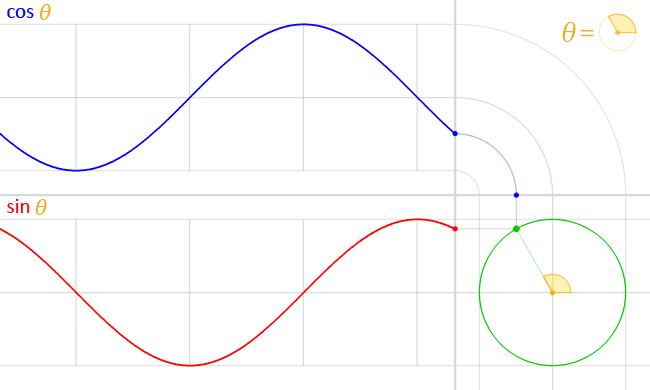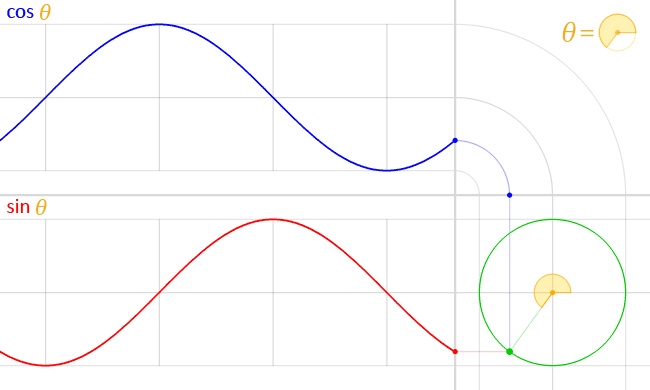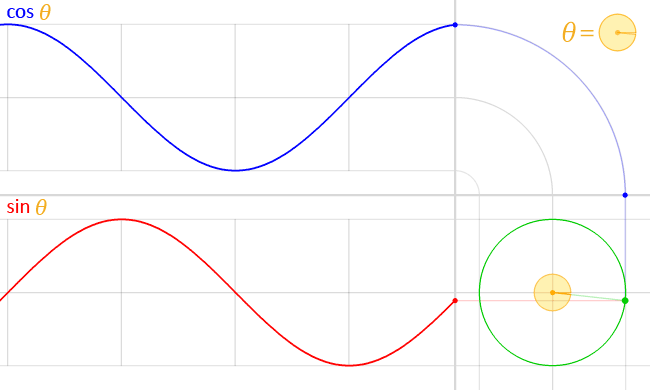
Die Animation zeigt: Bei der Spule im Wechselstromkreis eilt der Strom der Spannung nach. In der idealen Spule um 90°, wie am Winkel der roten und blauen Linie innerhalb des grünen Kreises zu erkennen ist.
Mittels dem Ohmschen Gesetz, kann der sogenannte induktive Blindwiderstand berechnet werden.
Mittels Spannung und Strom:
`X_l=U/I`
Mittels Frequenz und Induktivität:
`X_l=2*pi*f*L`
Diese Formeln lassen sich natürlich auch umstellen:
Frequenz: `f=X_l/(2*pi*L)`
Induktivität: `L=X_L/(2*pi*f)`
Die Formeln lassen sich auch Kombinieren da sich beide auf `X_L` auflösen:
Spannung: `U=2*pi*f*L*I`
Strom: `I=U/(2*pi*f*L)`
Wirk- und Blindwiderstand

Wird ein Wirkwiderstand und ein Blindwiderstand (Ein Widerstand und eine Spule)
zusammengeschaltet (siehe Bild) müssen die Widerstände und Ströme speziell verrechnet werden
und können nicht einfach addiert werden.
Der resultierende Widerstand aus einem Wirkwiderstand und einem Blindwiderstand wird Scheinwiderstand genannt,
und hat das Formelzeichen Z.
`U_"ges"` ist die Gesammtspannung über `R` und `L`
`U_R` ist der Spannungsabfall am Widerstand `R`
`U_L` ist der Spannungsabfall an der Spule `L`.
Die Formel für die Gesammtspannung ist `U_"ges"=sqrt(U_R^2+U_L^2)`.
Die Selbe Formel findet Anwendung beim Scheinwiderstand:
`Z=sqrt(R^2+X_L^2)`.
Sind Strom und Spannung bekannt, so entspricht Z dem Widerstand der mit dem Ohmschen Gesetz errechnet werden kann:
`Z=U_"ges"/I`. Ist der Strom gesucht, so kann `I=Z/U_"ges"` verwendet werden.
Güte
Die Güte einer Spule beschreibt das Verhältnis zwischen induktivem Blindwiderstand und dem "normalen" Widerstand
des Drahtes der die Spule bildet: `Q=X_L/R_V`
Der Gütefaktor "Q" ist eine Dimensionslose Einheit.
`X_L` ist der induktive Blindwiderstand, und `R_V` der Widerstand des Drahtes.
Je grösser `X_L`, desto besser die Güte, je grösser `R_V`, desto schlechter die Güte.
Transformatoren

Bei einem Transformator redet man immer von einer primären und einer sekundären Seite.
Die primäre Seite ist die Seite bei der mittels Strom ein Magnetfeld aufgebaut wird,
und die sekundäre Seite ist die Seite in welcher Strom durch das Feld induziert wird.
Anders ausgedrückt, die primäre Seite ist mit der Spannungsquelle verbunden,
und die sekundäre Seite mit dem Verbraucher.
In einem idealen Transformator ist die Spannung perfekt proportional zur Wicklungszahl
und der Strom perfekt umgekehrt proportional.
Daher gelten die Regeln in der folgenden Tabelle.
| Formel | Bedeutung |
|---|---|
| `P_P=P_S` | Die Leistungen der primären und sekundären Seite sind identisch |
| `ü=N_P/N_S` | Das Übertragungsverhältnis ist das Verhältnis zwischen Primär- und Sekundärwicklung |
| `ü=U_P/U_S` | Die Spannung ist proportional zur Wicklungszahl |
| `ü=I_S/I_P` | Der Strom ist umgekehrt proportional zur Wicklungszahl (Man bemerke der Sekundärstrom ist über dem Bruch) |
| `ü^2=R_P/R_S` | Das Quadrat des Übertragungsverhältnises ist proportional zu den Widerständen |
| `ü^2=L_P/L_S` | Das Quadrat des Übertragungsverhältnises ist proportional zu den Induktoren |
| `ü^2=C_S/C_P` | Das Quadrat des Übertragungsverhältnises ist umgekehrt proportional zu den Kapazitäten (Man bemerke die Sekundärkapazität ist über dem Bruch) |
"P"=Primär, "S"=Sekundär, "ü"=Übertragungsverhältnis
Hinweis: Damit ein Magnetfeld eine Spannung induzieren kann muss sich dieses Feld ändern. Das bedeutet, dass ein Transformator nur mit Wechselspannung funktioniert.
Weitere Eigenschaften
Die Grösse des Transformatorkernes richtet sich primär nach der Frequenz und der benötigten Leistung.
Ein zur Übertragung von 4000 Watt geeigneter Transformator wiegt beispielsweise:
bei 50 Hz etwa 25 kg
bei 125 kHz dagegen nur 470 g.
In modernen Netzteilen wird die Netzspannung gleichgerichtet, und anschliessend wird diese Gleichspannung mittels einem rapide wechselndem Schalter zurück in Wechselspannung umgewandelt, aber mit massiv erhöhter Frequenz. Diese Netzteile nennt man deswegen "Schaltnetzteile". Der Schalter in diesen Geräten ist pur elektronisch. Ein Schaltnetzteil besitzt keine beweglichen Teile.