Kondensatoren
Kondensatoren sind elektronische Bauteile welche eine Ladung speichern, und wieder freigeben können.
Funktionsweise
Ein Kondensator entsteht wenn zwei Leiter nahe beieinander liegen, aber durch ein isolierendes Medium (z.B. Luft oder Plastik) voneinander getrennt sind. Beim isolierenden Medium ist zu beachten, dass es polarisierbar ist. Dies bedeutet, dass das Medium keinen elektrischen Strom leitet, sich die Moleküle aber durch ein elektrisches Feld ausrichten ("polarisieren") lassen. Solche Materialien bezeichner man als Dielektrikum.
Wird an einem Leiter eine positive Ladung angebracht,
polarisiert dieser das Dielektrikum.
Dessen Moleküle richten sich nun so aus, dass die negative Seite zum positiv geladenen Leiter zeigt.
Dies hat zur Folge, dass die positive Seite zum gegenüberliegenden Leiter ausgerichtet ist,
und dadurch negative Ladungen in diesem anzieht.
Wird der Stromkreis unterbrochen verbleibt der Kondensator im geladenen Zustand,
da sich die Ladungen in den gegenüberliegenden Leiter nach wie vor anziehen.
Der Kondensator entlädt sich wieder sobald die beiden Enden miteinander verbunden werden,
da alle Ladungen das Bestreben haben sich auszugleichen.
Bauarten
Kondensatoren können auf verschiedene Weisen gebaut werden, und nicht jede Bauart ist für jede Anforderung geeignet. Elektrolyt Kondensatoren sind eine beliebte Bauform, da sie für ihr Volumen eine vergleichsweise hohe Kapazität aufweisen. Diese Kondensatoren verlieren jedoch mit dem Alter an Kapazität. Keramik Kondensatoren werden als SMD Komponente auf Leiterplatten aufgelötet, und neigen dazu ihre Kapazität sehr lange zu halten.
Polarisierung
Die meisten Kondensatorentypen sind nicht polarisiert, das heisst man kann sie in eine beliebige richtung in eine Schaltung einbauen. Polarisierte Kondensatoren (z.B. Elektrolytkondensatoren) müssen korrekt orientiert in die Schaltung eingebaut werden. Bei solchen Kondensatoren ist die positive und/oder negative Seite markiert am Gehäuse.
Kapazität
Die Fähigkeit eines Kondensators Ladungen zu speichern wird als Kapazität bezeichnet. Je höher die Kapazität, desto stärker lässt sich der Kondensator aufladen. Die Kapazität eines Kondensators ist von drei Faktoren abhängig:
-
Dielektrizitätszahl: Diese gibt an wie gut ein Dielektrikum geeignet ist.
Je höher, desto besser isoliert es die Platten und desto stärker lässt es sich polarisieren.
Die Zahl fungiert als Multiplikator zur Dielektrizitätskonstante
(siehe Formelsammlung).
Formelzeichen: `epsilon_r`
Einheit: Dimensionslos -
Plattenfläche: Je grösser die Platten, desto grösser die Kapazität.
Formelzeichen: A
Einheit: m2 -
Plattenabstand: Je kleiner der Abstand, desto grösser die Kapazität
Formelzeichen: `l`
Einheit: m
Die Kapazität wird mittels folgender Formel berechnet:
`C=epsilon_0*epsilon_r*A/l`
Die Kapazität hat die Einheit Farad (F),
die Einheit ist jedoch oft sehr klein,
häufig sind Mikro-, Nano-, und Picofarad.
Das Formelzeichen ist ein grosses C,
nicht zu verwechseln mit dem kleinen c,
welches für die Lichtgeschwindigkeit steht.
Die Formel zeigt uns, dass die Kapazität grösser wird wenn die Plattenfläche grösser wird
und/oder der Plattenabstand kleiner wird.
Kondensator am Gleichstrom

Es spielt keine Rolle ob der Widerstand vor, oder nach dem Kondensator in der Schaltung ist.
Ein Kondensator gilt als geladen nach `5*tau` Sekunden.
Bei der Ladung folgt der Strom einer logarithmischen Kurve.
Zuerst ist der Strom sehr gross, nimmt aber mit der Zeit ab.
Die gemessene Spannung über dem Kondensator folgt einer gespiegelten Kurve.
Die Berechnung der Spannung zu einem bestimmten Wert erfolgt mittels
`U_C=U*(1-e^(-t/tau))` wobei `U` die Endspannung ist, `e` die Eulersche Zahl (siehe Formelsammlung),
`t` die Zeit in Sekunden, und `tau` die Zeitkonstante.
Wird Spannung und Strom während dem Laden aufgezeichnet, so entstehen folgende Graphen:

Aus dieser Grafik ist ersichtlich, dass Spannung und Strom sich umgekehrt zueinander verhalten. Wird die maximale Spannung und der Maximale Strom auf einer Skala von 0%-100% gezeichnet, so ergibt die Summe zu einem Zeitpunkt jeweils 100%. Ist der Kondensator also 30% geladen, fliesst ein Ladestrom der 70% des Maximalstromes beträgt.
Prozentualwerte für Tau
| `tau` | Strom | Spannung |
|---|---|---|
| ≈0.7 | 50% | 50% |
| 1 | 36.8% | 63.2% |
| 2 | 13.5% | 86.5% |
| 3 | 5% | 95% |
| 4 | 1.8% | 98.2% |
| 5 | 0.7% | 99.3% |
Diese Tabelle und die Grafik oberhalb gelten für das Laden und Entladen beim Gleichstrom. Beim Laden sind die Zahlen und Grafik für Strom und Spannung exakt wie angegeben. Beim Entladen ist die Grafik für den Strom wie angegeben. Die Spannung ist umgekehrt da Spannung beim Entladen abgebaut und nicht aufgebaut wird. 63.2% bei 1 tau bedeutet hier, dass das Bauteil so viel Spannung bereits abgebaut hat.
Serielle und parallele Schaltungen
Serielle und parallele Schaltungen von Kondensatoren werden exakt umgekehrt gerechnet wie serielle und parallele Schaltungen von Widerständen. Dies bedeutet, dass sich die Kapazitäten von Kondensatoren in parallelen Schaltungen addieren. Bei seriellen Schaltungen kann eine von drei Formeln verwendet werden
Einfache Formel
`C=C_1/n`
Diese Formel funktioniert wenn alle seriellen Kondensatoren die exakt selbe Kapazität haben. In diesem Falle ist `C_1` die Kapazität einer der Kondensatoren und `n` die Anzahl der Kondensatoren.
Formel für zwei Kondensatoren
`C=(C_1*C_2)/(C_1+C_2)`
Immer noch relativ einfach zu rechnen, funktioniert auch wenn die beiden Kondensatoren verschiedene Kapazitäten haben, aber nur wenn es exakt zwei Kondensatoren sind.
Universale Formel
`C=1/(1/C_1+1/C_2+...)`
Diese Formel funktioniert für eine beliebige Anzahl an Kondensatoren mit beliebigen Kapazitäten.
Tip: `1/n` ist das Selbe wie `n^-1`. Die Formel oberhalb kann also umgeschrieben werden auf
`C=(C_1^-1+C_2^-1+...)^-1`. Diese Form ist ggf. einfacher in den Taschenrechner einzugeben.
Wechselspannung
Kondensatoren im Gleichstromkreis erreichen ihren vollen Lade-, oder Entladezustand nach ca. 5 Tau. Im Wechselstromkreis ändert sich der Ladezustand eines Kondensators kontinuierlich. Da der Lade-, und Entladestrom eines Kondensators nicht immer gleich ist, sondern vom Ladezustand abhängig ist, fungiert dieser wie ein sich dynamisch verändernder Widerstand.
Zeichnet man Spannung und Strom im Wechselstromkreis über Zeit auf,
so entsteht der hier gezeigte Verlauf,
wobei blau der Strom ist, und rot die Spannung.
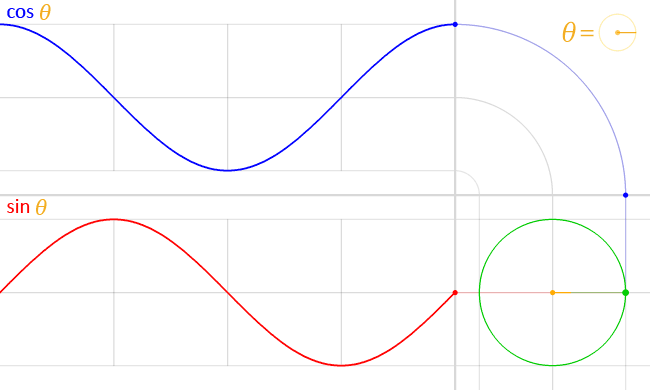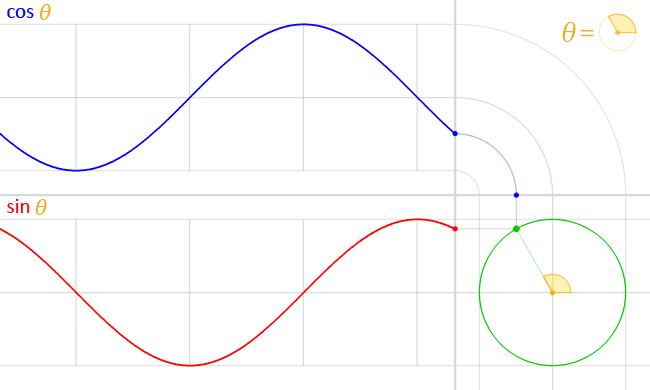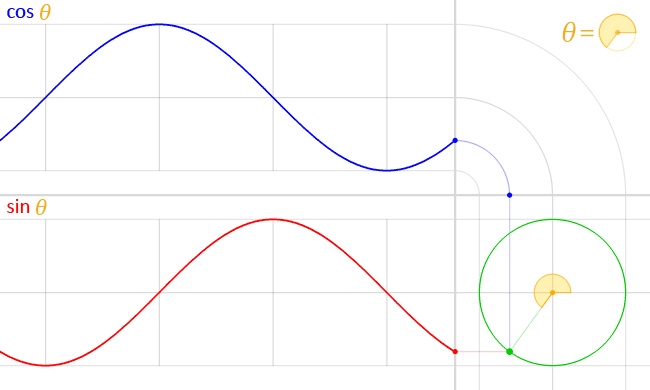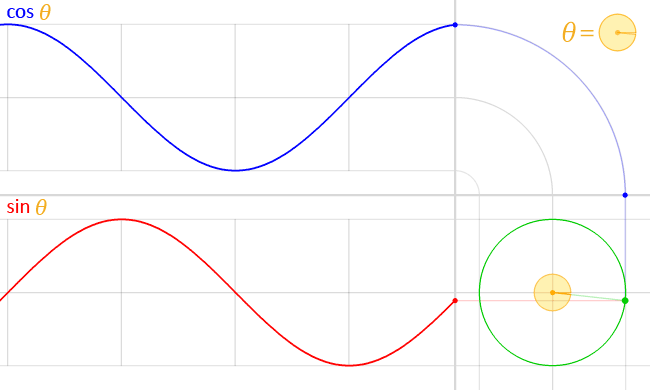
Die Animation zeigt: Beim Kondensator im Wechselstromkreis eilt der Strom der Spannung voraus. Im idealen Kondensator um 90°, wie am Winkel der roten und blauen Linie innerhalb des grünen Kreises zu erkennen ist.
Mittels dem Ohmschen Gesetz, kann der sogenannte kapazitive Blindwiderstand berechnet werden,
wenn Spannung und Strom bekannt sind:
`X_c=U/I`
Alternative Formel mittels Frequenz und Kapazität:
`X_c=1/(2*pi*f*C)`
Diese Formeln lassen sich natürlich auch umstellen:
Frequenz: `f=1/(2*pi*X_c*C)`
Kapazität: `C=1/(2*pi*X_c*f)`
Die Formeln lassen sich auch Kombinieren da sich beide auf `X_c` auflösen:
Spannung: `U=1/(2*pi*f*C)*I`
Strom: `I=U/(1/(2*pi*f*C))`
Wirk- und Blindwiderstand

Wird ein Wirkwiderstand und ein Blindwiderstand (Ein Widerstand und ein Kondensator)
zusammengeschaltet (siehe Bild) müssen die Widerstände und Ströme speziell verrechnet werden
und können nicht einfach addiert werden.
Der resultierende Widerstand aus einem Wirkwiderstand und einem Blindwiderstand wird Scheinwiderstand genannt,
und hat das Formelzeichen Z.
`U_"ges"` ist die Gesammtspannung über `R` und `C`
`U_R` ist der Spannungsabfall am Widerstand `R`
`U_c` ist der Spannungsabfall am Kondensator `C`.
Die Formel für die Gesammtspannung ist `U_"ges"=sqrt(U_R^2+U_c^2)`.
Die Selbe Formel findet Anwendung beim Scheinwiderstand:
`Z=sqrt(R^2+X_c^2)`.
Sind Strom und Spannung bekannt, so entspricht Z dem Widerstand der mit dem Ohmschen Gesetz errechnet werden kann:
`Z=U_"ges"/I`. Ist der Strom gesucht, so kann `I=Z/U_"ges"` verwendet werden.
Bereichseinengung
Bei einem verstellbaren Kondensator kann es teilweise notwendig sein das Verhältnis zwischen unterer und oberer Kapazität einzuengen damit es auf einen bestimmten Frequenzbereich passt. (Siehe Frage 3.36)
Für eine Bereichseinengung wird ein Kondensator parallel geschaltet, damit sich die Anfangs- und Endkapazität des verstellbaren Kondensators erhöhen. Das Kapazitätsverhältnis ist identisch dem Quadrat des Frequenzverhältnis: `V_f^2=V_c`
Zuerst muss das Frequenzverhältnis und das existierende Kapazitätsverhältnis ausgerechnet werden:
Kondensator: `V_c=C_e/C_a`
Frequenz: `V_f=f_o/f_u`
Parallelkapazität: `C_p=(C_e-V_c*C_a)/(V_c-1)`
Als eine Formel: `C_p=(C_e-(f_o/f_u)^2*C_a)/((f_o/f_u)^2-1)`