Schwingkreise

Ein Schwingkreis ist eine Schaltung die in ihrer einfachsten Form aus einem Kondensator und einer Spule besteht. Diese Schaltung kann entweder seriell oder parallel ausgelegt sein

Funktionsprinzip

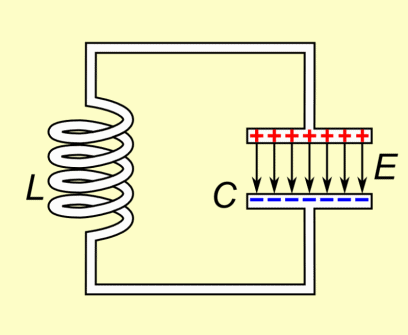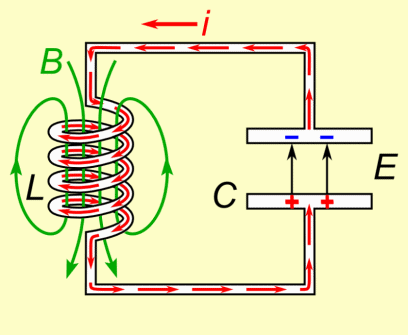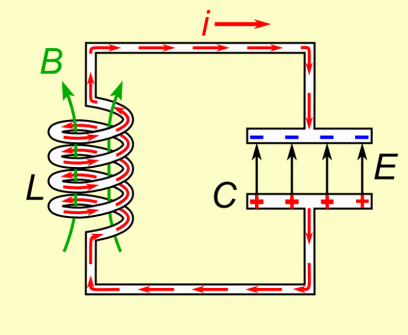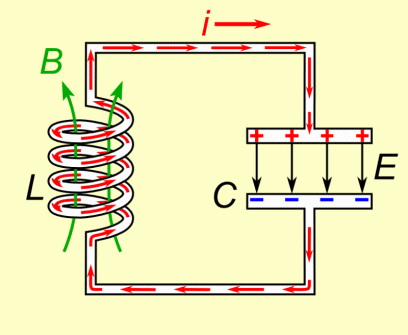
Wird ein geladener Kondensator mit einer Spule zusammengeschaltet, so entlädt sich der Kondensator durch die Spule. Die Spule baut dabei ein Magnetfeld auf und begrenzt die Geschwindigkeit des Entladevorganges. Ist der Kondensator entladen findet kein Stromfluss mehr statt der das Magnetfeld aufrecht erhält. Dieses bricht nun zusammen und entlädt sich zurück in den Kondensator. Der Stromfluss ist hierbei immer noch in die selbe Richtung wie beim Aufladen der Spule. Der Kondensator lädt sich also in umgekehrter Polarisierung nun auf. Ist die Spule komplett entladen und das Magnetfeld aufgelöst kann sich der Kondensator erneut durch die Spule entladen, nun fliesst der Strom aber in die andere Richtung.
Dieser Vorgang wird theoretisch unendlich lange wiederholt. In the Praxis entstehen Verluste, insbesondere in den Leitungen und dem Draht der Spule, wodurch der Vorgang eventuell gestoppt wird, da die verfügbare Energie in der Schaltung bei jedem Stromfluss etwas kleiner wird. Den selben Effekt gibt es auch ausserhalb der Elektronik. Eine Stimmgabel wird nach dem Anschlagen auch immer leiser, da durch den Luftwiderstand sowie den internen Widerstand im Material Verluste entstehen.

Serielle Schaltungen

Bei seriellen Schaltungen sind Spule und Kondensator hintereinander geschaltet.
Die Spule hat bei niedrigen Frequenzen nur einen geringen Widerstand und lässt diese mit nur wenig Hindernis passieren. Bei hohen Frequenzen wiederum sperrt sie immer mehr, je höher die Frequenz wird. Der Kondensator wiederum lässt hohe Frequenzen mehrheitlich ungehindert passieren, während er gegenüber tieferen Frequenzen immer mehr sperrt.
"Sperren" hier bedeutet, dass die Komponente einen hohen Widerstand hat.

Zeichnet man den Spannungsabfall über der Schaltung bei immer höher werdenden Freuqnz auf, so entsteht folgender Graph:

Der Graph zeigt, dass der Spannungsabfall bei sehr kleiner Frequenz gross ist. Wird die Frequenz erhöht, wird der Spannungsabfall kleiner da der Kondensator durchlässiger wird. Bei genügend hoher Frequenz wird die Spule sperrend und der Spannungsabfall steigt wieder an.
Der Punkt `f_0` wo der Spannungsabfall sein minimum erreicht ist der Punkt in dem die Schaltung in Resonanz arbeitet.

Verwendung

Je nach dem, wie diese Schaltung in eine grössere Schaltung integriert wird kann sie eine bestimmte Frequenz sperren, oder durchlassen. Wird die Schaltung in Serie zum Signal geschaltet, so fungiert es als ein Bandpass. Wird die Schatung parallel geschaltet, z.B. zwischen Antenne und Erdung, so schliesst sie eine bestimmten Frequenzbereich kurz, und entfernt diesen vom Signalspektrum. In dieser Form nennt man dies auch einen Saugkreis, da die Schaltung ein bestimmtes signal "ansaugt".

Parallele Schaltungen

Bei parallelen Schaltungen sind Spule und Kondensator nebeneinander geschaltet.
Niedrige Freqenzen passieren einfach durch die Spule, und hohe Frequenzen einfach durch den Kondensator. Mittlere Frequenzen müssen durch beide Komponenten mit Hinderniss, und daher findet dann ein grosser Spannungsabfall statt.

Zeichnet man den Spannungsabfall über der Schaltung bei immer höher werdenden Freuqnz auf, so entsteht folgender Graph:

Der Graph zeigt, dass der Spannungsabfall bei sehr kleiner Frequenz klein ist. Wird die Frequenz erhöht, wird der Spannungsabfall grösser, da weder Kondensator noch Spule für mittlere Frequenzen sehr durchlässig sind. Bei genügend hoher Frequenz wird der Kondensator durchlässig und lässt hohe Frequenzen passieren.
Der Punkt `f_0` wo der Spannungsabfall sein maximum erreicht ist der Punkt in dem die Schaltung in Resonanz arbeitet.

Verwendung

Da diese Schaltung ein Spannungsbild zeigt, welches dem Gegenteil der Serienschaltung entspricht, sind die Verwendungszwecke auch gegenteilig.

Resonanz

Ein Schwingkreis arbeitet in Resonanz wenn `X_L=X_C`, also wenn der kapazitive und induktive Blindwiderstand identisch sind. In diesem Falle heben sich die meisten Eigenschaften der Komponenten gegenseitig auf. Da der Strom im Kondensator um 90° voraus eilt, und der Strom in der Spule um 90° nacheilt, sind diese um 180° voneinander unterschiedlich, zeigen also in die gegenteilige Richtung. Ist `X_C=X_L` ist dementsprechend auch `I_C=I_L`, die Ströme heben sich also auf, und ohne Stromfluss kein Spannungsabfall.
Die Schaltung selbst besteht dann nur noch aus dem Widerstand `R`, welcher für den Widerstand der Schaltung selbst steht, zum Beispiel dem Kabel oder des Drahtes in der Spule.

Ist eine Schaltung in Resonanz können die Widerstände mit `X_C=X_L=sqrt(L/C)` ausgerechnet werden.
Des weiteren kann die Resonanzfrequenz mittels `f_0=1/(2*pi*sqrt(L*C))` bestimmt werden.
Bei Resonanz gilt auch `Z=R`, dies bedeutet, dass der Strom und Spannung durch das Ohmsche Gesetz berechnet werden können.

Der Scheinwiderstand in einem Kondensator- und Spulenkreis kann auch ausgerechnet werden durch `Z=sqrt(R^2+(X_L-X_C)^2)`
Bei Resonanz gilt jedoch `X_L=X_C`, daher `X_L-X_C=0`, daher `Z=sqrt(R^2+0^2)`, daher `Z=sqrt(R^2)`, daher `Z=R`

Hinweis: `X_L-X_C` in obiger Rechnung kann ausserhalb der Resonanz negativ sein, dies Spielt aber keine Rolle, da `x^2` immer positiv ist, auch wenn `x<0` da die Multiplikation zweier negativer Zahlen immer positiv ist.

Güte

Genau wie eine Spule hat auch ein Schwingkreis eine Güte, diese kann je nach vorhandenen Werten mit vielen Formeln gerechnet werden:

Spannung: `Q=U_L/U_"ges"=U_C/U_"ges"`

Widerstand: `Q=X_L/R=X_C/R`

Kreisfrequenz: `Q=(2*pi*f*L)/R=1/(2*pi*f*C*R)=1/R*sqrt(L/C)`

Bandbreite: `Q=f_0/b`

Bandbreite

Jeder Schwingkreis hat eine bestimmte Bandbreite für die er durchlässig ist, häufig ist dies der Bereich bei dem eine Dämpfung von 0 dB bis 3 dB auftritt. Dies entspricht einer Signalstärke am Ausgang von 71% - 100% im vergleich zur Eingangsstärke. Die Differenz zwischen der höchsten und tiefsten Frequez die unter obigen Bedingungen noch passieren kann nennt man Bandbreite. Das stärkste Signal erzielt man normalerweise in der Mitte zwischen der unteren und oberen Frequenz. Beispiel: Ein Schwingkreis hat eine Bandbreite von 5 kHz, und die mittlere Frequenz ist 470 kHz. Dies bedeutet, dass die untere und obere Frequenz 465 kHz und 475 kHz sind.

Die Bandbreite kann auf verschiedene Arten berechnet werden

Durch die obere und untere Frequenz: `b=f_"oben"-f_"unten"`

Mittels der Hauptfrequenz und der Güte `b=f_0/Q`

Durch den Widerstand und Spule: `b=R/(2*pi*L)`

RL und RC Schaltungen

Der Kondensator oder Spule kann durch einen Widerstand ersetzt werden. In diesem Falle kann die Grenzfrequenz (3dB Punkt) bestimmt werden durch folgende Formel:

Kondensator: `f=1/(2*pi*R*C)`

Spule: `f=R/(2*pi*L)`